Matematika

Fraktály

Fraktál je geometrický objekt, jehož základní vlastností je tzv. soběpodobnost:
to znamená, že pokud daný útvar pozorujeme v jakémkoliv měřítku, vidíme stále se opakující určitý charakteristický motiv.

Fraktály mívají na první pohled složitý tvar, ale jsou generovány opakovaným použitím jednoduchých matematických pravidel.

Fraktály se hojně vyskytují v přírodě: sněhové vločky, řeky, cévní systém, stromy, kapradiny, ...

Dimenze fraktálu

Specifickou vlastností fraktálů je, že jejich fraktální dimenze neodpovídá jejich topologické dimenzi:
máme-li normální křivku jako třeba úsečku, nebo kružnici, můžeme určit její délku. Fraktál vzniká nekonečnou rekurzí a délka této křivky může být nekonečná.

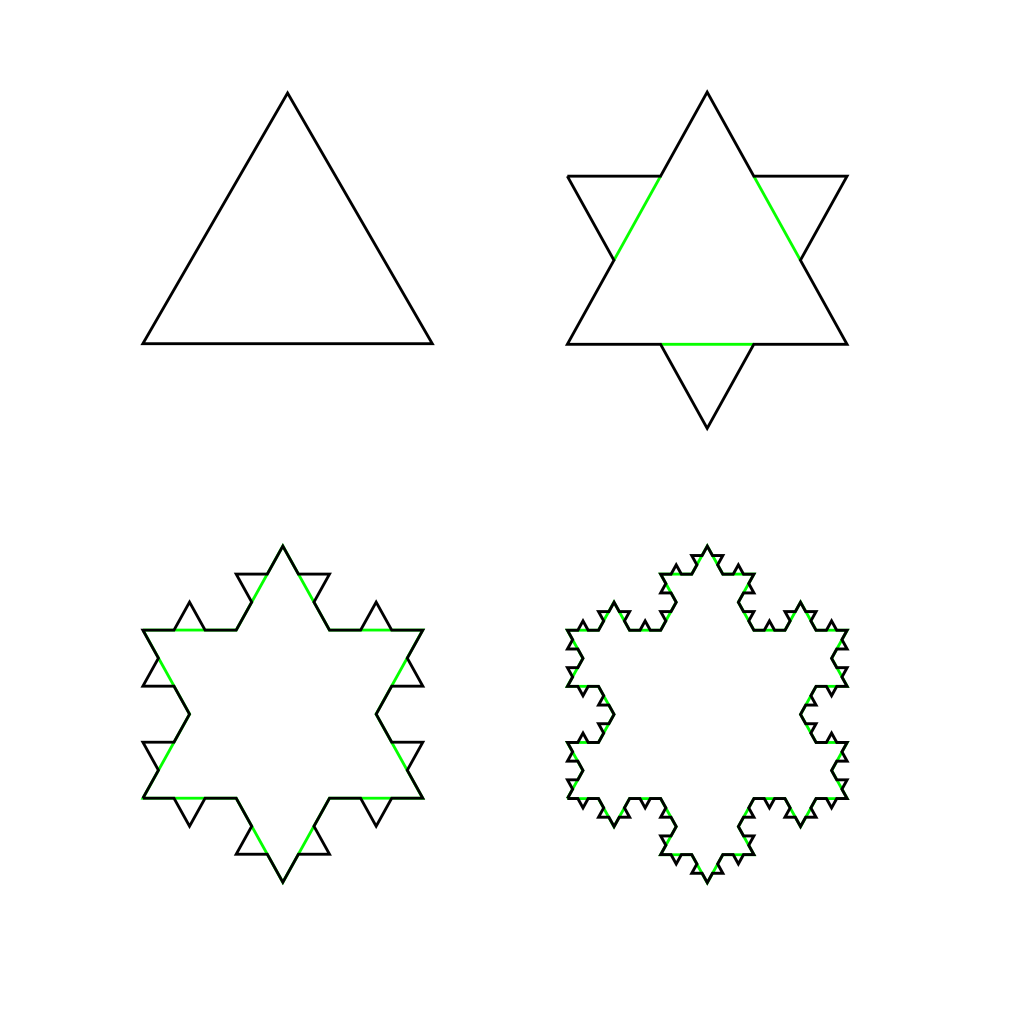
Jako příklad můžeme vzít Kochovu křivku:

Její délka se v každém kroku prodlouží vždy o třetinu. Z toho vyplývá, že po n -tém kroku bude délka křivky (4/3)ⁿ délky původní úsečky. Délka této křivky je tedy nekonečná.

Pokud je křivka uzavřená, tvoří tzv. Kochovu vločku. To je útvar s nekonečným obvodem, ovšem konečným obsahem: v každém kroku se sice plocha zvětšuje, ale přidávané trojúhelníky jsou čím dál menší a výsledkem je konvergentní geometrická řada. Obsah Kochovy vločky je roven 8/5 obsahu původního trojúhelníka.

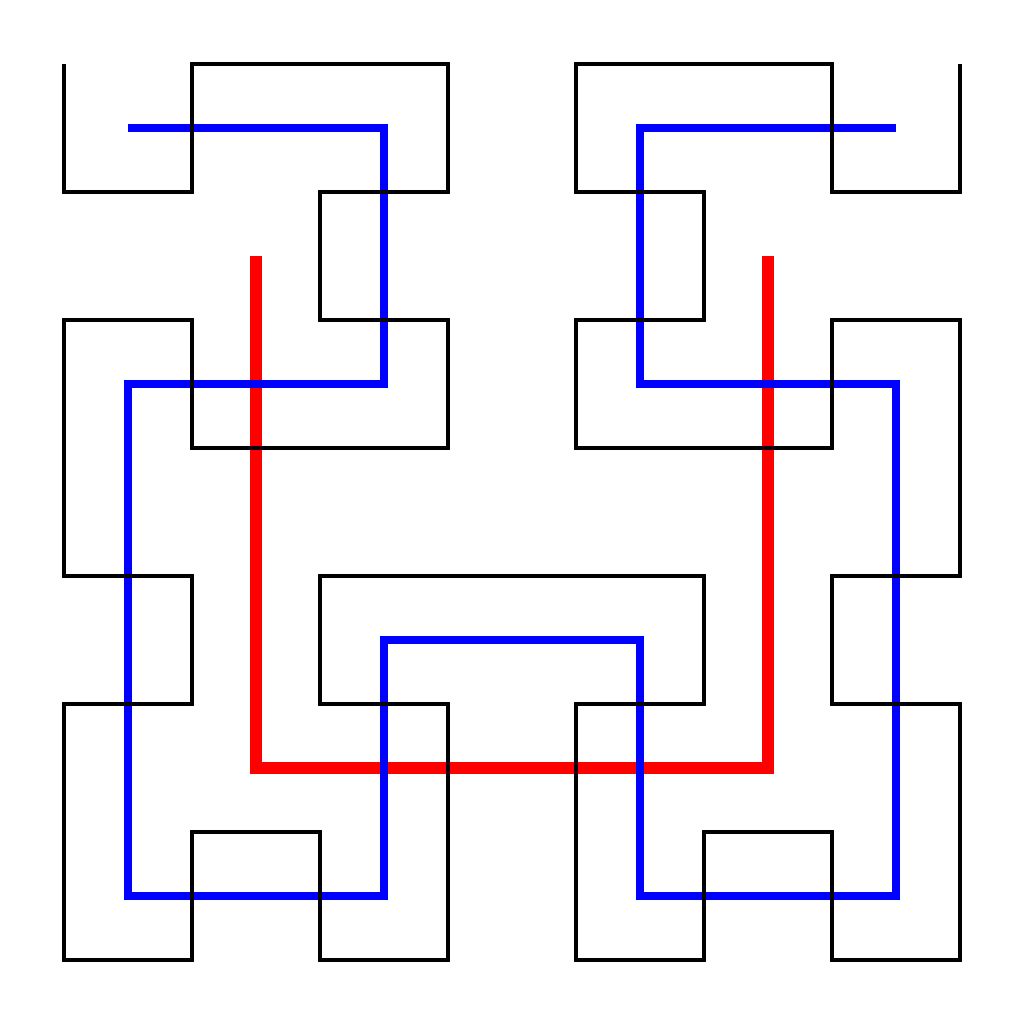
Existují rovněž křivky, které se nikde nekříží a přesto bezezbytku vyplní plochu - např. Peanova křivka či Hilbertova křivka. Jsou to tedy křivky či plochy? Tedy mají dimenzi 1 nebo 2?

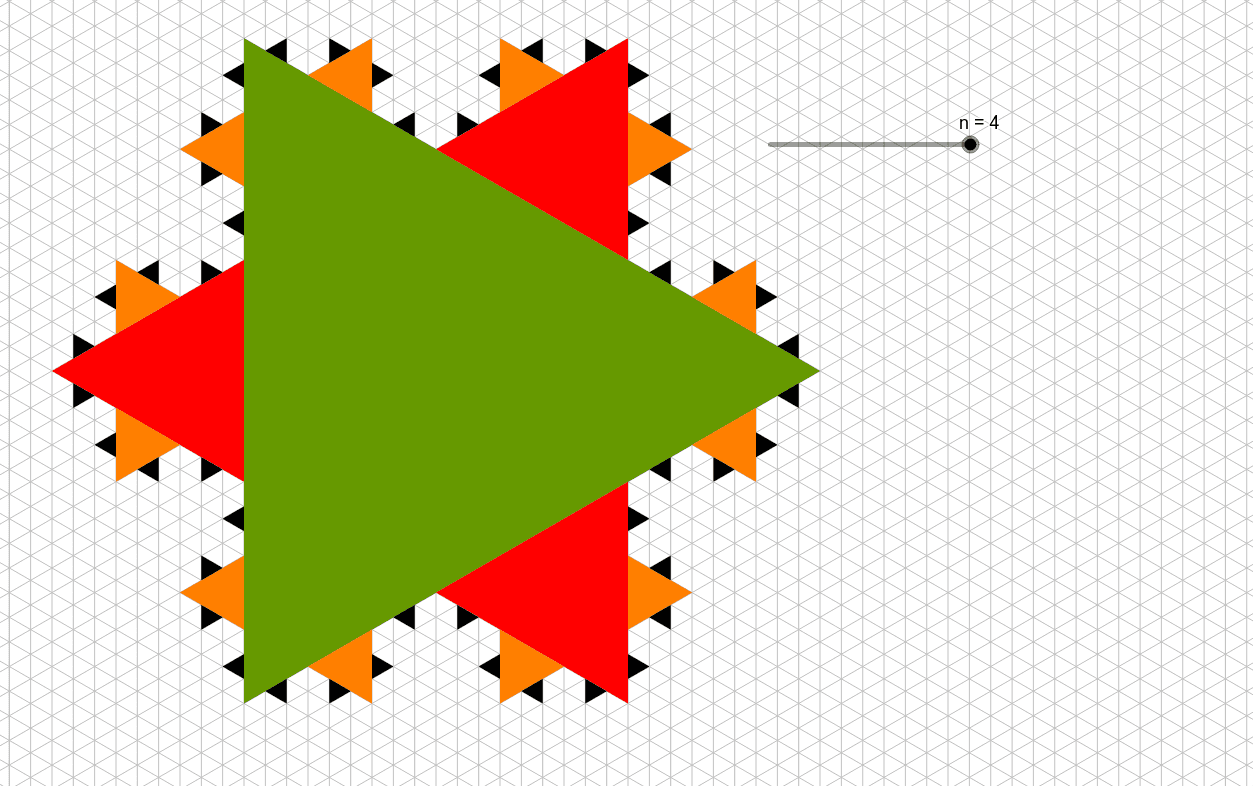
Obdobný zmatek způsobují fraktály - plochy, jako příklad vezměme Sierpińského trojúhelník. Trojúhelník je jasně plošný útvar, který má svůj obsah. Jaký je ale obsah Sierpińského trojúhelníku? Když budeme z trojúhelníků odebírat donekonečna středové trojúhelníky, zbudou nám nakonec jen body s nulovým obsahem.

Proto vznikly různé způsoby, jak definovat dimenzi těchto útvarů. Nejznámější je Hausdorffova dimenze.

Hausdorffova dimenze se určí zhruba tak, že se podíváme, s jakým faktorem se útvar dělí a o kolik se v každém kroku zvětší.

Hausdorffova dimenze Kochovy křivky je ln 4 / ln 3 ≈ 1,26 ... úsečku rozdělíme na tři díly a prodlouží se na čtyři (Kochova křivka zaplňuje rovinu více než pouhá přímka s dimenzí 1, ale nezaplňuje ji úplně).

Křivky vyplňující prostor jako Peanova křivka mají stejný Hausdorffův rozměr jako prostor, který vyplňují.

Sierpinského trojúhelník je spojením tří kopií sebe sama, přičemž každá kopie je zmenšena o faktor 1/2. Má tedy dimenzi ln 3 / ln 2 ≈ 1,58.