Matematika

Problémy milénia

1. Problém P versus NP
2. Hodgeova domněnka
3. Poincarého domněnka
4. Riemannova hypotéza
5. Yangova-Millsova teorie a hypotéza hmotnostních rozdílů
6. Navierovy-Stokesovy rovnice
7. Birchova a Swinnertonova-Dyerova domněnka

Poincarého domněnka

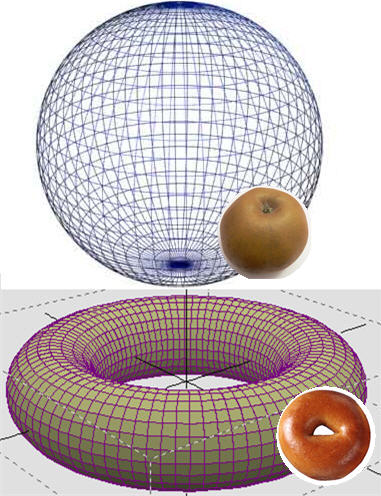
Domněnka tvrdí, že každý jednoduše souvislý trojrozměrný povrch je ekvivalentní povrchu čtyřrozměrné koule.

Jako jediná z problémů tisíciletí byla již vyřešena. Důkaz podal roku 2003 Grigorij Perelman; jeho správnost byla potvrzena v srpnu 2006.

Grigorij Perelman

• V roce 2006 dostal prestižní Fieldsovou medailí, matematickou obdobou Nobelovy ceny. Cenu však odmítl.
• V roce 2010 odmítl rovněž převzetí finanční prémie ve výši 1 000 000 USD za vyřešení jednoho ze sedmi matematických problémů tisíciletí.
• V prosinci 2005 odstoupil Grigorij Perelman ze svého postu vedoucího výzkumného pracovníka v laboratoři matematické fyziky a téměř úplně přerušil kontakty s kolegy.
• V září 2011 matematik odmítl přijmout nabídku stát se členem Ruské akademie věd.
• Vede osamocený život, ignoruje tisk. Žije v Petrohradu v Kupchinu se svou matkou.