Pascalův trojúhelník
Pascalův trojúhelník je struktura přirozených čísel daná uspořádáním podle určitých pravidel:- boční strany trojúhelníku tvoří vždy číslo 1
- čísla uvnitř trojúhelníku jsou vždy součtem dvou čísel ležících nad daným políčkem
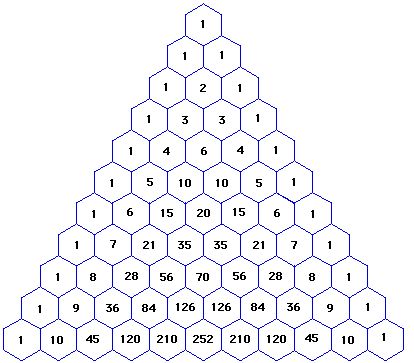
Jak uvidíte dále, je Pascalův trojúhelník cosi jako kalkulačka, a proto si v úlohách v odkazu určitě vyzkoušejte, zda umíte tuto geniální kalkulačku používat.
- Čísla v trojúhelníku jsou tzv. binomické keficienty:

Kombinační číslo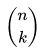 je matematická funkce, která udává počet možností, jak vybrat k prvků z n-prvkové množiny.
je matematická funkce, která udává počet možností, jak vybrat k prvků z n-prvkové množiny.
(Máte k dispozici jablko, hrušku, banán a kiwi. Chcete dát dítěti k svačině 2 kusy ovoce. Kolik máte možností? V tomto případě 4 nad 2 = 6 ... jablko + hruška, jablko + banán, jablko + kiwi, hruška + banán, hruška + kiwi, banán + kiwi).
Stejná čísla dostanete, pokud roznásobíte závorky (a + b)n:- (a + b)1 = 1 * a + 1 * b
- (a + b)2 = 1 * a2 + 2 * a * b + 1 * b2
- (a + b)3 = 1 * a3 + 3 * a2 * b + 3 * a * b2 + 1 * b3
- (a + b)4 = 1 * a4 + 4 * a3 * b + 6 * a2 * b2 + 4 * a * b3 + 1 * b4
- ...
- Součet čísel v řádku Pascalova trojúhelníku je roven mocninám čísla 2:
- řádek 1 = 20 = 0
- řádek 1 + 1 = 21 = 2
- řádek 1 + 2 + 1 = 22 = 4
- řádek 1 + 3 + 3 + 1 = 23 = 8
- řádek 1 + 4 + 6 + 4 + 1 = 24 = 16
- ...
- Podívejme se na strany trojúhelníka:
- v první řadě jsou čísla 1
- ve druhé řadě jsou čísla 1, 2, 3, ..., n
- ve třetí řadě jsou tzv. trojúhelníková čísla, neboli součty čísel od 1 do n
Jeden z prvních, kdo používal trojúhelníková čísla, byl Karl Friedrich Gauss, který je použil ve škole, když mu bylo devět let. Učitel žákům udělil práci, ve které měli počítat 1+2+3+…+1000. Po chvíli se Karl Gauss přihlásil se správným řešením. Udělal to tak, že vypočítal 1000·1001:2 = 500500.
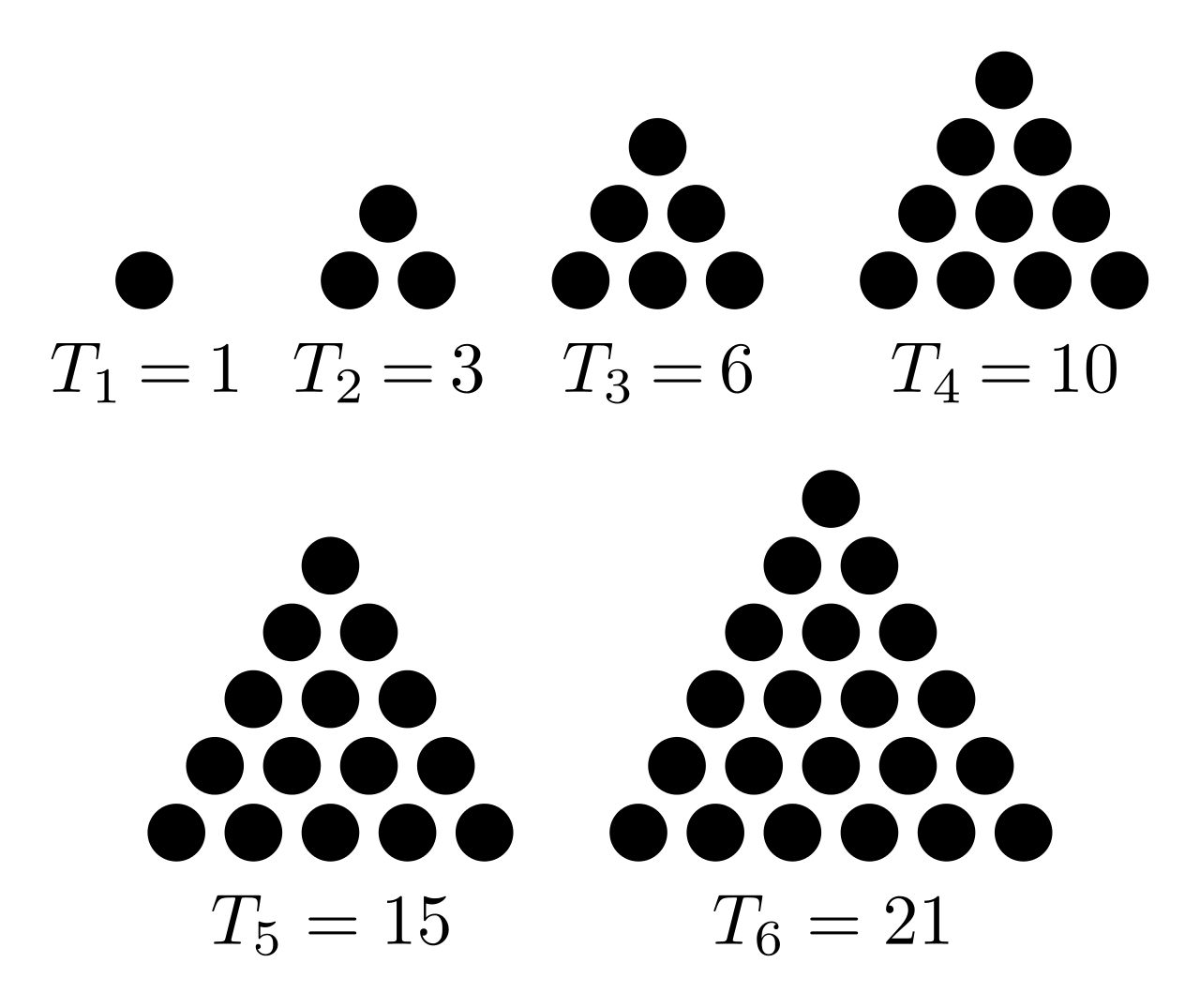
Z obrázku je vidět, proč se těmto číslům říká trojúhelníková - je jich vždycky tolik, že je lze uspořádat do plného trojúhelníku. - ve čtvrté řadě jsou tzv. tetraedrická čísla, tj. počet bodů tvořících pravidelný čtyřstěn.

- Fibonacciho posloupnost:

Diagonální součty (označené červeně) v Pascalově trojúhelníku jsou Fibonacciho čísla (1, 1, 2, 3, 5, 8, 13, 21, 34, ...)
- Číslice řádku Pascalova trojúhelníku tvoří (po drobném výpočtu) mocniny 11:
- řádek 1 = 110
- řádek 1 1 = 111
- řádek 1 2 1 = 112
- řádek 1 3 3 1 = 113
- řádek 1 4 6 4 1 = 114
- řádek tvoří čísla 1 5 10 10 5 1 - zde začíná problém, musíme si nějak poradit s čísly 10. Uděláme to tak, že dvojciferná čísla trochu přeskládáme: 1 (5+1) (0+1) 0 5 1 = 161051 = 115
- řádek 1 6 15 20 15 6 1 → 1 (6+1) (5+2) (0+1) 5 6 1 = 1771561 = 116
- Lichá a sudá čísla Pascalova trojúhelníku tvoří fraktál tzv. Sierpińského trojúhelník.


(1623 – 1662)
Blaise Pascal byl francouzský matematik, fyzik, spisovatel, teolog a náboženský filozof.

(cca 1180 – 1250)
Leonardo Fibonacci (také známý jako Leonardo Pisano) byl středověký italský matematik. Významně podpořil rozšíření používání arabských číslic v Evropě. Je po něm pojmenována Fibonacciho posloupnost.

(1777 – 1855)
Carl Friedrich Gauss byl slavný německý matematik a fyzik. Zabýval se mimo jiné geometrií, matematickou analýzou, teorií čísel, astronomií, elektrostatikou, geodézií a optikou. Mezi jeho stěžejní díla patří spis Disquisitiones Arithmeticae, který napsal již ve věku 21 let. Tato práce položila základy teorie čísel jakožto matematické disciplíny.